加速寿命测试中常用的失效分布模型主要包括以下几类，它们适用于不同的失效机理和数据特征：
1. 指数分布（Exponential Distribution）
特点：
无记忆性（失效概率与时间无关）。
失效率恒定（λ），适用于早期随机失效或电子元件的寿命分析。
应用场景：
电子元器件（如电阻、电容）的寿命测试。
简单系统或组件的早期失效分析。
公式：
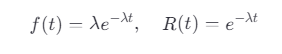
λ：失效率（尺度参数）。
2. 威布尔分布（Weibull Distribution）
特点：
β < 1：早期失效（如制造缺陷）；
β = 1：随机失效（类似指数分布）；
β > 1：耗损失效（如疲劳、老化）。
灵活性强，可通过形状参数（β）描述不同失效阶段：
适用于复杂失效模式（如机械部件、电子器件）。
应用场景：
机械部件（轴承、齿轮）的疲劳失效；
电子产品的电迁移失效；
加速寿命测试中多阶段失效分析。
公式：
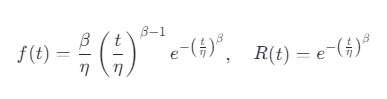
η：尺度参数（特征寿命）；
β：形状参数（失效阶段判定）。
3. 正态分布（Normal Distribution）
特点：
对称分布，适用于机械磨损类失效（如材料疲劳、尺寸变化）。
失效时间围绕均值对称分布。
应用场景：
机械部件的疲劳寿命测试（如弹簧、螺栓）；
需要精确预测寿命均值和方差的场景。
公式：
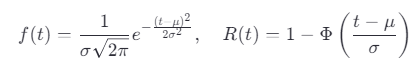
μ：均值（平均寿命）；
σ：标准差（寿命离散程度）。
4. 对数正态分布（Lognormal Distribution）
特点：
对数变换后服从正态分布，适用于失效时间与对数变量相关的场景（如腐蚀、扩散过程）。
尾部较长，适合描述缓慢增长的失效过程。
应用场景：
化学腐蚀（如金属氧化层退化）；
材料疲劳（如裂纹扩展）。
公式：
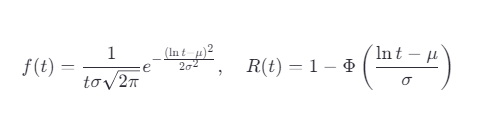
μ：对数均值；
σ：对数标准差。
5. Gumbel 分布（极值分布 I 型）
特点：
用于极值分析（如最大/最小失效时间）。
在加速失效时间模型（AFT）中常与指数分布或威布尔分布结合使用。
应用场景：
极端环境下的寿命预测（如高温、高压测试）；
指数回归模型和威布尔回归模型的基础。
公式：
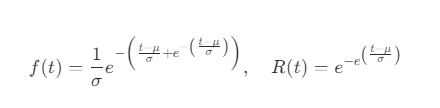
μ：位置参数；
σ：尺度参数。
6. Logistic 分布
特点：
尾部比正态分布更重，适合描述寿命分布具有长尾特征的场景。
在加速失效时间模型中用于构建对数logistic回归模型。
应用场景：
生物医学设备的寿命分析；
失效时间受多重因素影响的场景。
公式：
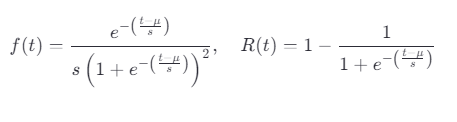
μ：位置参数；
s：尺度参数。
7. 广义极值分布（Generalized Extreme Value Distribution, GEV）
特点：
统一了极值分布 I 型、II 型和 III 型，适用于不同类型的极值失效分析。
应用场景：
极端环境下的寿命预测（如航空航天设备）。
8. 二项分布（Binomial Distribution）
特点：
用于截尾试验（如定数截尾样本）的失效次数统计。
应用场景：
加速寿命测试中故障数的统计分析（如抽样检验）。
公式：
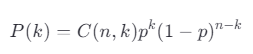
n：样本总数；
p：单次试验的失效概率。
选择失效分布模型的关键因素
失效机理：
机械磨损（正态/对数正态） vs. 电子失效（威布尔/指数）。
数据特征：
是否存在早期失效（β < 1）或耗损失效（β > 1）。
测试目标：
需要预测平均寿命（正态/对数正态）还是可靠性置信区间（威布尔）。
实际案例
威布尔分布：
案例：汽车轴承的疲劳寿命测试。
结果：通过威布尔分布的形状参数 β = 2.5 判断为耗损失效，优化润滑设计后 β 降低至 1.8。
指数分布：
案例：LED 驱动电源的高温加速测试。
结果：失效率为 λ = 0.001/h，推算 MTBF = 1000 小时。
总结
在加速寿命测试中，威布尔分布和指数分布是最常用的失效分布模型，因其灵活性和广泛的适用性。选择时需结合失效机理、数据特性和测试目标，并通过统计检验（如卡方检验、Kolmogorov-Smirnov 检验）验证模型的适用性。